﹀
﹀
本文标题中的债务雕刻(Debt Sculpting)其本质上是一种本金偿还的计算方法,使得债务的本金偿还与项目产生的现金流的相一致。在预测项目的未来的现金流之后,根据可用于还款的现金流以及银行要求的最低偿还备付率确定融资规模。具体的概念以及计算方法将在后文中详细介绍。
在介绍债务雕刻在模型中的计算方法之前,我们需要先了解偿债备付率(Debt Service Coverage Ratio,后文简称为DSCR)这一概念。DSCR是项目融资中使用最广泛的债务比率,在融资关闭前可以用于确定债务规模,在融资关闭后可以评估是否允许企业分红等。
DSCR是“可用于还款的现金流”(Cash Flow Available for Debt Service,等于息税折旧摊销前利润(EBITDA)减去所得税,后文简称为CFADS)和“当期应还本付息额”的比率,这个比率大于1,意味着当期产生的现金可以覆盖全部的本息支出,如果小于1则说明当期产生的现金不足以还本付息。
在项目融资时,银行会对DSCR提出最低要求,以保证项目的现金流足以在规定期限内偿还全部债务,并根据最低的DSCR确定可以贷出本金。最低DSCR的确认是根据项目类型、企业评级、收入可靠程度等,来判断项目或企业的综合风险情况。
举个例子,在电力项目中收入会分为签署购电协议收入(电价确定性高、风险低)和市场售电收入(电价波动大、风险高),融资的时候银行一般会根据收入的确定性提出最低DSCR要求,比如购电协议部分的收入的DSCR可能是1.3x左右,市场收入的DSCR可能是1.7x左右,每年综合的最低DSCR也是随两种收入比例的变化而波动的,比如前期购电协议和市场部分的收入各占比50%,那么DSCR就是1.5x左右,后期市场收入占比达到80%,那么DSCR就是1.6x左右。
在日常建模中,比较简单的还款方案是等额本金和等额本息,这个在财务模型中是很好实现的,但是等额本金和等额本息并不是“最优解”,因为这两种还款是根据项目的本金来预测还款金额的,而不是根据项目的实际情况,如果项目的现金流前低后高,可能会有现金不足的情况。
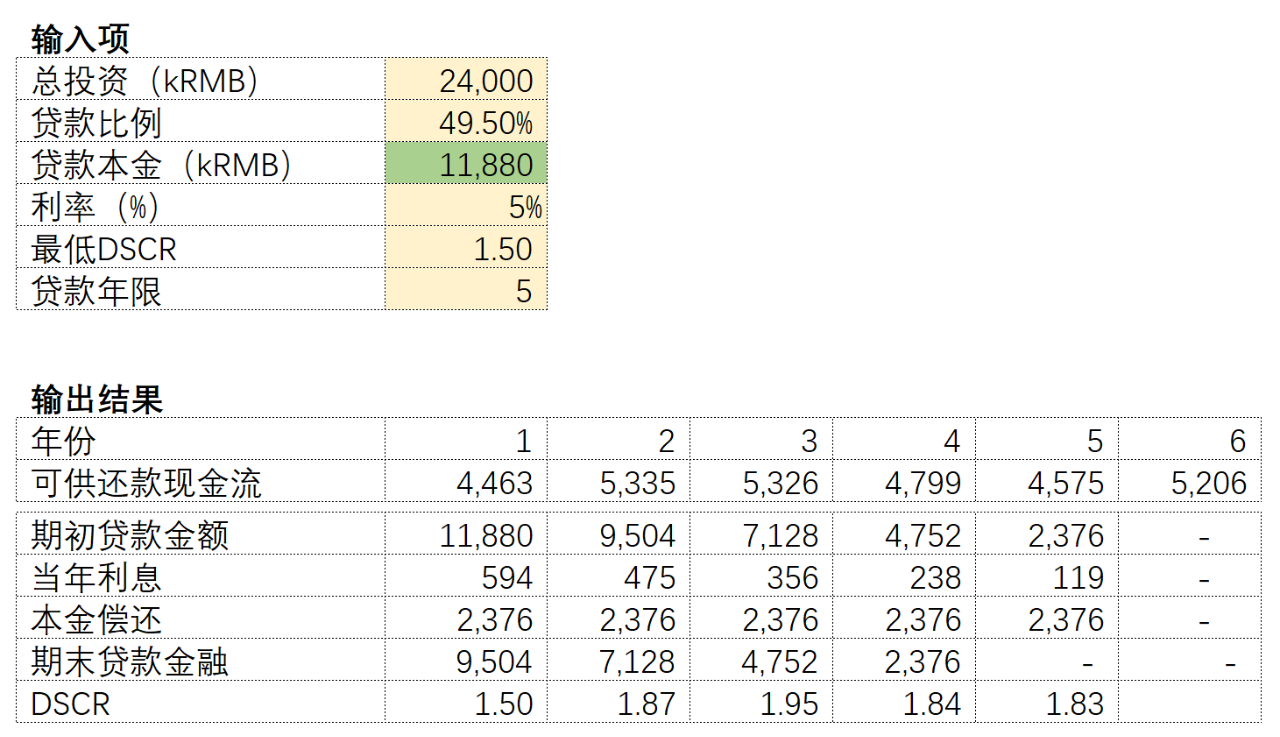
我们举个例子,并用这个例子贯穿全文来介绍债务雕刻的计算方法。一个项目总投资2400万人民币,现在需要申请一笔贷款,DSCR的最低要求是1.50x,贷款年限是5年,利率是5%(假设不变)。可供还款的现金流如下表。
如果采用等额本金且满足DSCR的情况下,贷款比率不能超过49.5%,以保证贷款期间DSCR满足银行的最低要求。
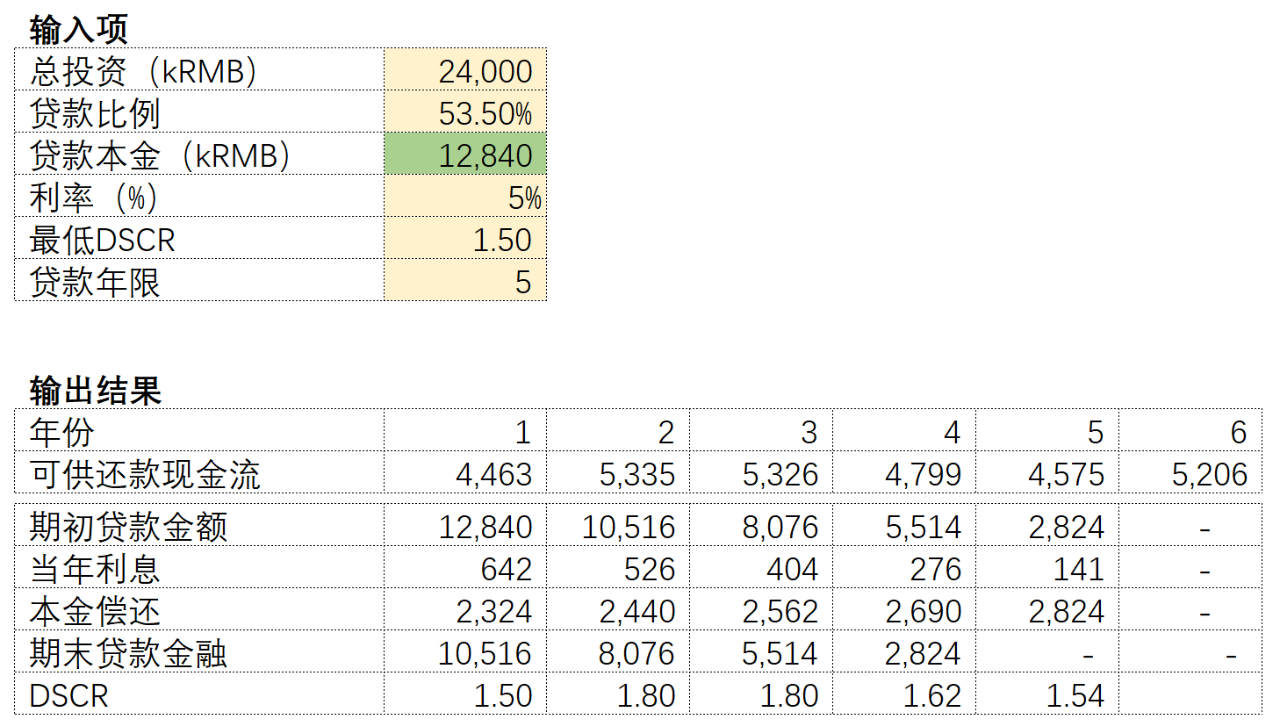
如果是采用等额本息且满足DSCR的情况下,贷款比率则不能超过53.5%。
但是在实际企业经营的时候,企业会根据项目进展情况以及企业收益的情况灵活调整还款计划,在项目收益较差的阶段少还款,从而提高资金利用效率,在项目收益好的阶段多还款,可以降低融资成本。
如果我们采用雕刻还款,该项目的贷款比例又是多少呢?具体是多少,让下面这三种方法来帮我们在Excel中解答吧!
债务雕刻这一概念被广泛应用在项目融资的财务模型中。在使用不同的三种方法之前,要先梳理一下模型的逻辑。首先对DSCR进行公式变形,用CFADS除以DSCR,得到当期用于偿还债务本金和利息的现金总和;在这个数上减去利息,就可以得到当期的“本金”。每一期的“本金”之和,就是期初的贷款本金,但是如果按照这个逻辑放在Excel里,就会出现循环引用的问题,为了解决循环引用的问题,总结了以下三种方法:
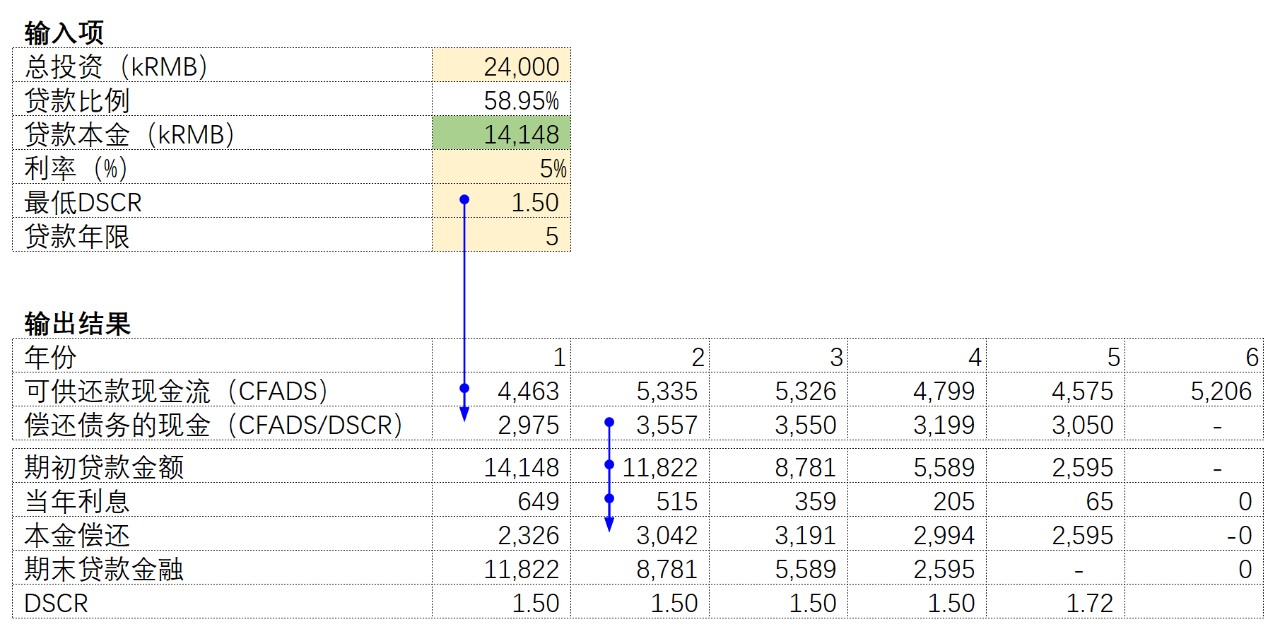
在贷款期限内,利率是固定的情况下,可以使用NPV(或XNPV)公式,NPV是计算净现值的公式,以贷款利率为贴现率,计算每期偿还贷款的现值,就可以得到项目的期初的贷款本金。在贷款本金的格子中输入“=NPV(利率,贷款期内可用于偿还债务的现金流)”。
这种方法的优点就是简单,简单的有点作弊的感觉,连还贷款的公式都不用调整,缺点是有一个很重要的前提条件,就是贷款的利率是固定的,如果贷款的利率是随浮动利率而变化的,就没法使用这种方法去做债务雕刻。
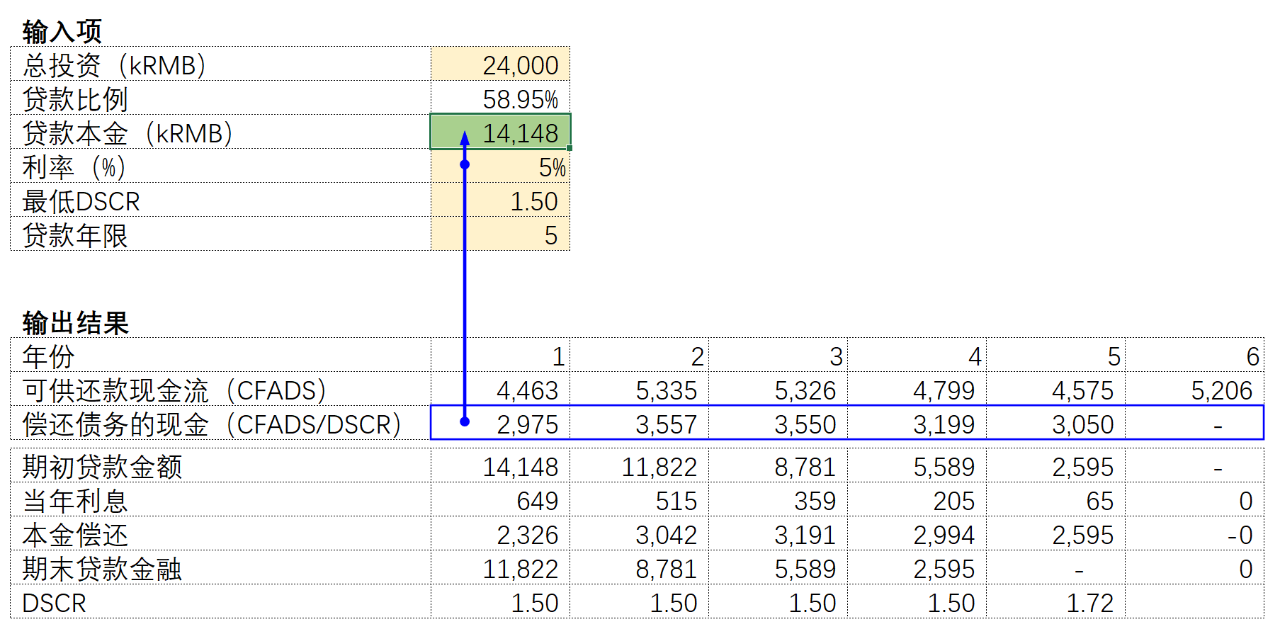
这种简单的NPV计算有几个限制条件,首先就是利息是按照期初的贷款金额计算的,此外利息是固定的,如果利率是变化的,比如每年上涨0.2%,或者利息要根据贷款的期初期末平均值计算,就需要尝试方法二和方法三进行债务雕刻的计算。
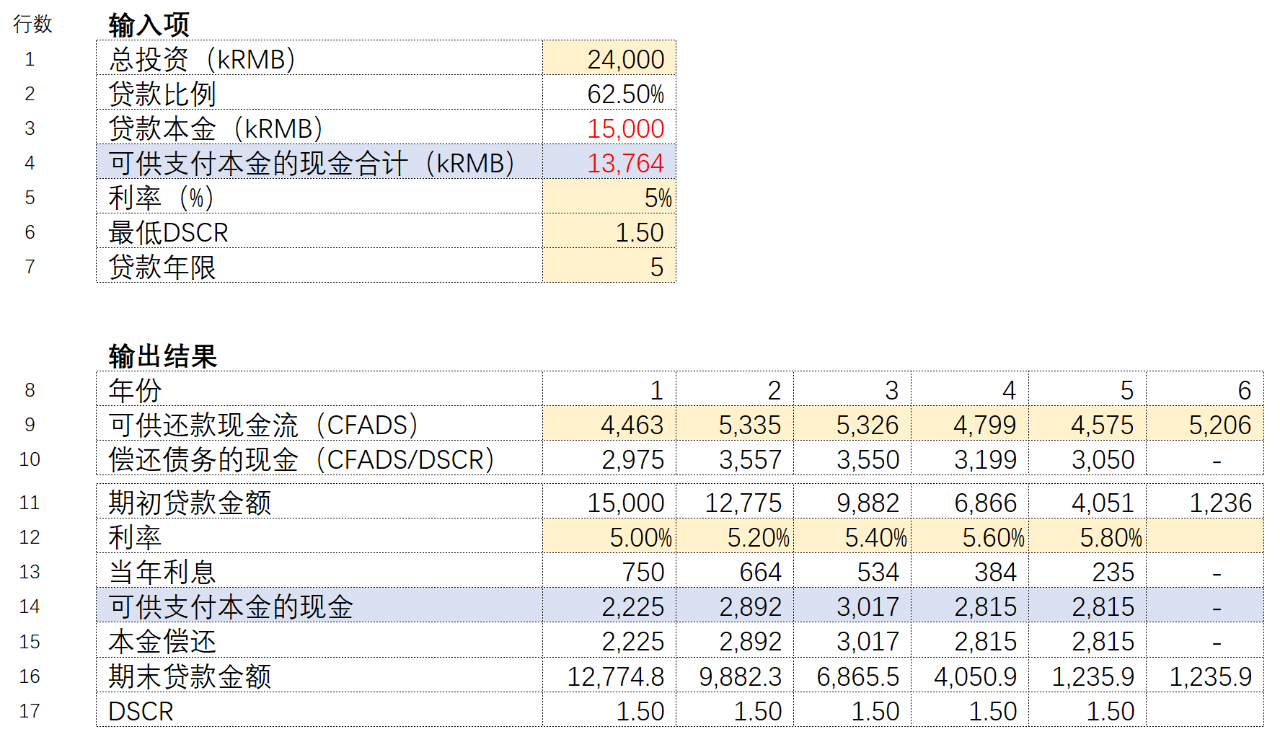
因为循环是出现在本金、利息计算、本金偿还这三者之间的,所以要利用复制粘贴数字来切断他们之间的循环计算。需要加两行内容,一是根据偿还债务现金(CFADS/DSCR)减去当期的利息,计算出来当期可供偿还本金的金额,二是将这些金额(第15行)加总作为可供还款现金合计,如下图中标蓝的两行(行数4、行数15)。在第三行的贷款本金处先随便输入一个数字,比如下图所示的“15000”,此时会出现贷款在5年内无法还清的情况,且可用支付本金的现金合计(行数4)低于贷款本金(行数3)。反之,如果是输入较少的贷款金额则会出现可用支付本金的现金合计(行数4)高于贷款本金(行数3)的情况,在贷款结束的年份会有额外的可供支付本金的现金。但是不论贷款金额是高是低,都可以通过下面的操作,计算出“最优解”。
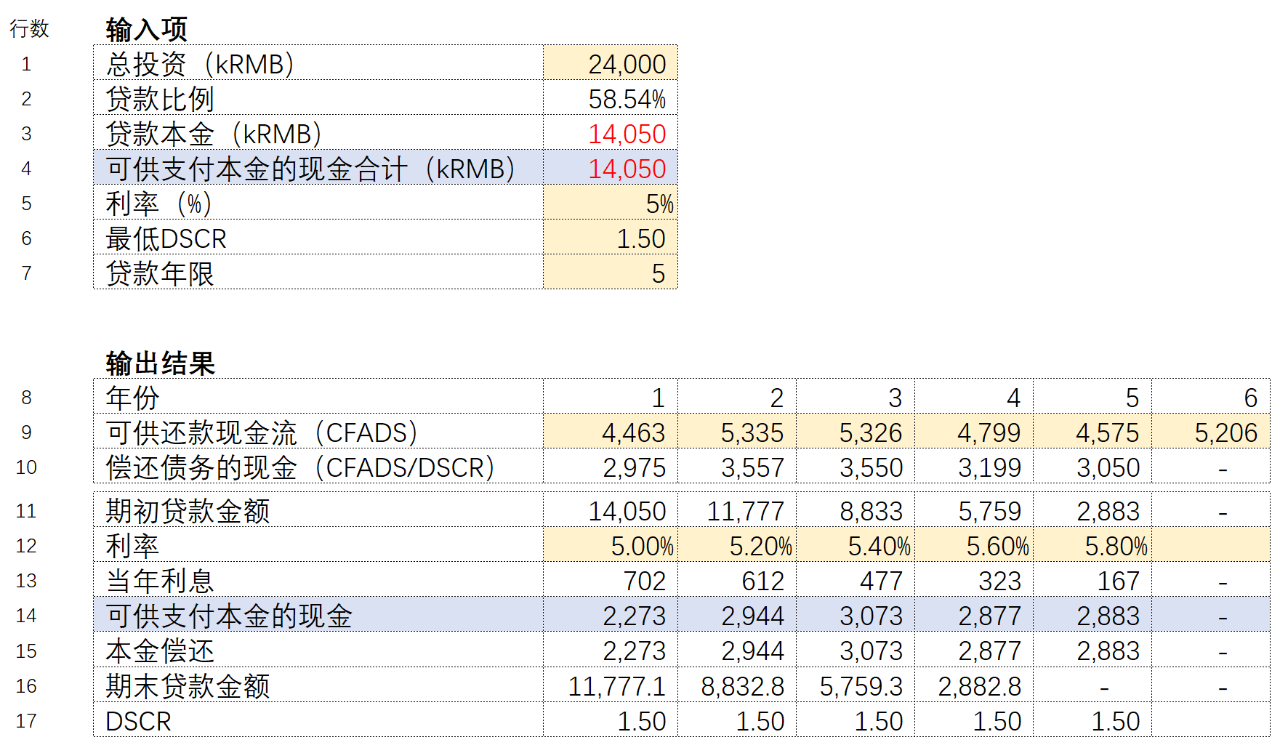
在不使用宏的情况,可以“手动”实现计算,复制可供还款现金合计的数字(行数4),粘贴纯数字到贷款本金中(行数3),粘贴之后发现可供还款现金合计的数字(行数4)的数字会本金的变化而变化,重复上面的复制粘贴,大概10次左右,数字就不再变化,而且贷款在第六年还清,且每期的本金偿还等于可供还款现金。
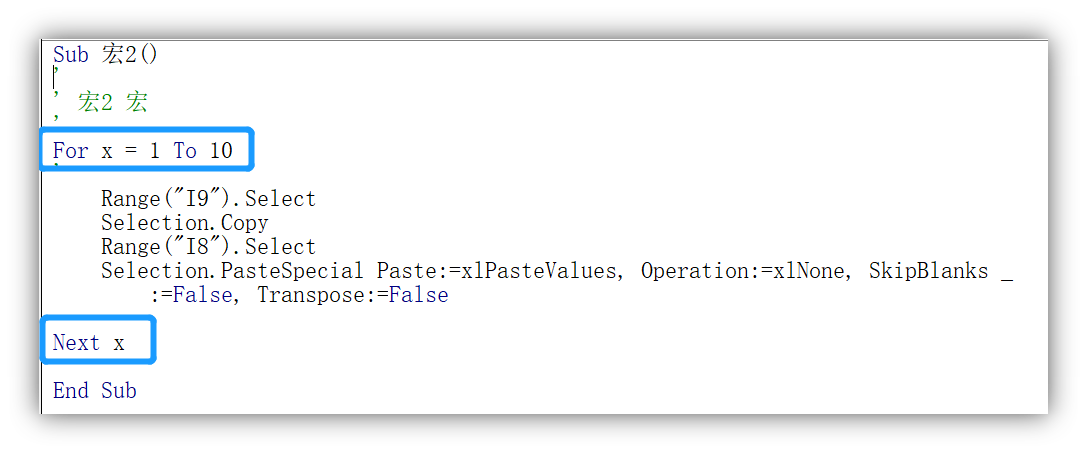
如果是需要在宏中实现则需要录制一次刚才复制粘贴的操作,具体宏的代码如下,如果录制时有其他操作,可以在宏中编辑删除。但是因为要大概重复10次刚才的复制粘贴工作才能确保数字没有变动,所以可以在宏上增加一个重复的语句(蓝色框中),就可以实现重复操作10次了。
不仅仅是贷款雕刻,在其他的循环计算中也可以使用这种方式切断循环。但是有没有什么方法可以在不使用宏的情况下,实现非固定利率的贷款雕刻呢?查找书籍后发现了方法三。
这种方法是基于预测的现金流去倒算贷款本金,如果贷款期限是5年,那么第五年期末的贷款金额就是0,就是从第五年的现金流开始往回计算总共可以贷出多少钱。这种算法的核心逻辑就是债务计算的时间顺序是反着的。正常在计算债务本息的时候,期初贷款金额等于上一期的期末值,期末贷款金额等于期初的减去当年的本金偿还。这种方法下是贷款结束时的贷款期末金额为0,当年的期初的价值等于期末价值加回当期的本金偿还。具体的步骤以及公式推到可以按照后面的公式进行带入:
第一步:贷款期末金额公式调整。
债务到期时贷款期末金额为0,其余年份为下一年的贷款期初值。先使用IF公式(=if(年份=贷款年限,1,0))增加时间旗帜确定债务到期日,然后再使用IF公式(=if(当年的还款年份flag=1,0,下一年期初贷款金额))将债务到期时的贷款调整为0,其余年份等于下一年期初的贷款金额。
第二步:贷款期初金额公式调整。
因为一般情况下,期初贷款金额会等于上一年的期末贷款金额,所以我们经过上一步调整之后会出现循环引用的问题,根据倒挤这个思维逻辑,这里我们要把当期期初的金额调整为当期的期末值+当期的本金偿还。
第三步:利息计算调整。
调整了期初和期末金额后,利息和本金的计算出现了循环引用。我们需要先把利息计算的公式变形:
原公式:当年利息=当年期初贷款金额ⅹ当年的利率
变形后公式:当年利息= (当期的期末贷款金额+当期的本金偿还)ⅹ当年的利率
这里利息的计算是根据期初本金,如果是根据期末和期初的平均值的话,当年的利息的计算就要再变形(当年利息= (当期的期末贷款金额+0.5ⅹ当期的本金偿还)ⅹ当年的利率)。
第四步:本金偿还的计算调整。
跟利息的计算一样,本金计算公式也需要变形,具体的推导如下:
原公式:
偿还债务的现金(CFADS/DSCR)= 利息 + 本金偿还
本金偿还 = 偿还债务的现金- 利息
本金偿还 = 偿还债务的现金- (期末贷款金额+本金偿还)ⅹ当年的利率
本金偿还+本金偿还ⅹ当年的利率 = 偿还债务的现金- 期末贷款金额ⅹ当年的利率
变形后公式:
本金偿还 =(偿还债务的现金- 期末贷款金额ⅹ当年的利率)/ (1+当年的利率)
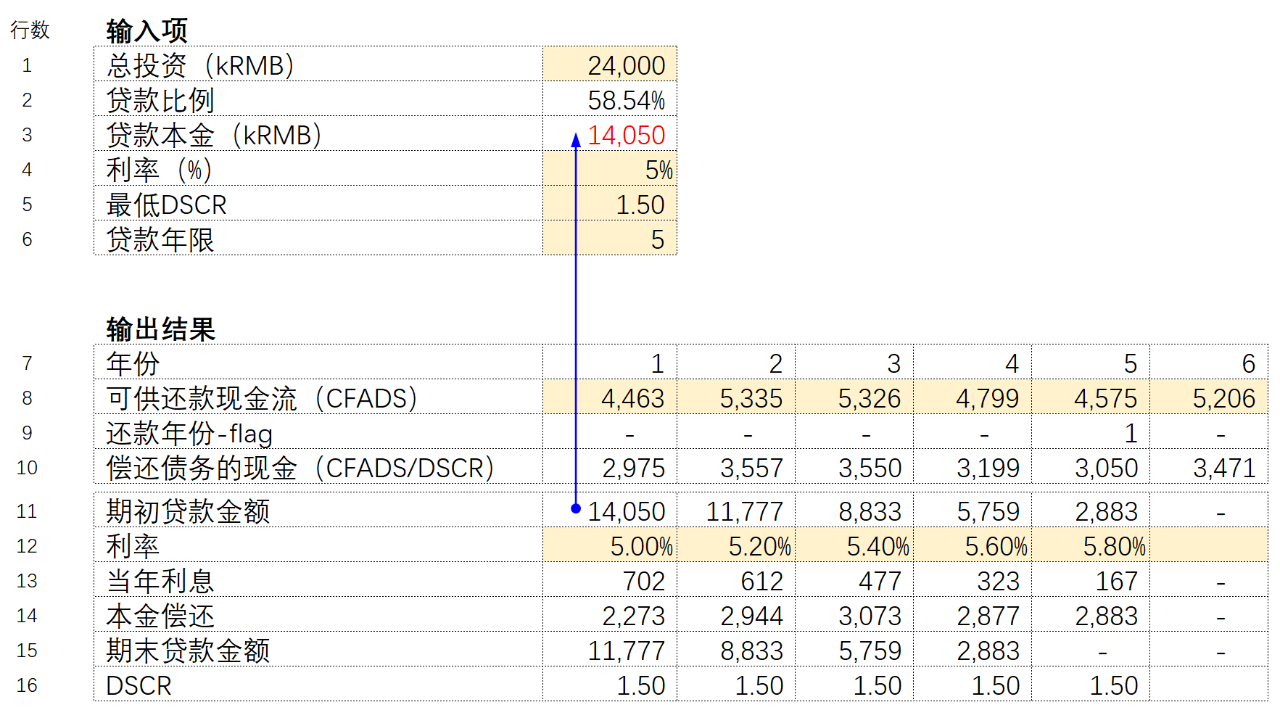
根据上述四步更新公式后,就可以计算出首年的期初贷款金额,这就是贷款的本金了。如果大家还想更深一步了解和学习雕刻法的建模方法,可在后台回复:财务模型进阶 5折购买财务模型经典图书。
作者简介:
Lisa Wei
注册估值师(CVA),CFA,注册估值师(CVA)协会专家委员会成员,现就职于某央企海外新能源开发部门,九年投资工作经验,八年新能源行业估值投资经验,曾就职于世界500强能源类外企以及能源类央企,参与多起海内外项目并购,曾担任估值培训以及注册估值师(CVA)培训讲师。
以上文章仅代表作者个人观点,不代表本公众号立场。未经授权,请勿以任何形式进行转载。